前回、ベイズ導入とベイズ統計的機械学習参考書の紹介など
で、筆者が考えうる限りもっとも簡潔なベイズ推定の概念導入を試みましたが、それなりの反応をいただきました。
やはり疑問、というか納得しにくい、納得した上で先に進みにくいのがベイズの定理であるようで、それが自然だとも思います。
「なんかひっかかる」「納得しにくい」という概念が現れたときは、そこは素通りすべきではないと思います。ほとんどの場合そこには大きな発想、パラダイムの転換(コペルニクス的転換)またブレイクスルーが存在していて、そこを突き詰めて考察することはとても有意義で楽しいことです。また逆にそういうパラダイムの差異を曖昧にしたまま腑に落ちないまま先に進むと苦労するのは自分だとも思います。
実際、ベイズ理論は、義務教育で習う統計学の発想、理念、哲学とは異なり、またイメージしにくいものだと思います。
義務教育で習うスタンダードな統計学は、ネイマンとピアソン、という人たちが体系構築したもので、「ネイマン=ピアソンの頻度主義統計学」とか呼ばれているようです。
彼らが思いっきり糾弾して表舞台(学会)から一旦放逐してしまった、近年大復活を遂げているのが、ベイズという人が考えたベイズ統計学というわけですが、何が異なるのか?
ここは実際かなり哲学的な思索になるわけで、筆者自身は結構そういうことは突き詰めて考えないと先に進みたくないわけで、自分なりに考えた結果、多分ほかではあんまり言われていない考え方をシェアしたいと思います。
キーワードは、現実(という世界)、観測、条件付き確率です。
1が出る可能性が100%のサイコロは存在するか?(歪みもないのに)
という思考実験をしてみます。
厳密な議論はさておき「ネイマン=ピアソンの頻度主義統計学」では、歪みがないんだから、無限回数試行(サイコロふってみること)をすれば、大数の法則で確率1/6に収束するはずだ、これが「真の確率」である、みたいなことを論じます。まあ学校でだいたいこういう感じで習ったと思います。そういうことです。
一方で、ベイズ統計学では確率とは「観測された事象」によって決まるという考え方をしています。
1が出る可能性が100%のサイコロは存在するか?(歪みもないのに)
答えYes。
たとえば、買ってきたばかりのサイコロをふって10回連続で1が出ることはあります。(1/6)の10乗の確率でそうなります。しかしそれは「極まれでたまたま」であって、次は1じゃないだろうとか100回ふったらさすがに1が出ないだろう、みたいになるわけですが、100回連続でふっても(1/6)の100乗の確率で「ありえる」わけです。
年末ジャンボ宝くじを1枚だけ買って、1等が当たる確率は2,000万分の1らしいですが、1枚だけ買っても当たる人は当たるわけで、その人にとっては当選確率100%になるわけです。だって当たったんだから。
「確率」というのは、「ネイマン=ピアソンの頻度主義統計学」のように、そういう人らが「こうだ」と厳密に定義することも可能ですが、別の解釈も可能な余地があるように思えます。「ネイマン=ピアソンの頻度主義統計学」は「客観確率」、「ベイズ統計学」はここで少し例を出した雰囲気からなんとなくわかるかもしれませんが「主観確率」と呼ばれたりします。
数学っていうのはもちろん、そもそも人間と関係なくアプリオリに存在していて、プラトンが論ずるように「イデア」として「客観」として存在しているわけで、その意味ではこの「主観確率」っていうのは何?ってことになります。少なくとも自分はこの「主観確率」っていう分類表現がどうも気に食わない。じゃあどう解釈するか?
ポイントは「観測」です。現代物理学、量子力学を勉強していると、どうもこの「観測」っていうのが「やっかい」もの扱いされているとわかってきます。
量子力学は、シュレディンガー方程式で記述される波動関数の確率密度によって量子の存在確率が決まるんですが、人間が観測した時点で、その波動関数っていうのは「崩壊」「収束」して1個の点に決まります。まあ、確率統計で構築されている美しい理論が、人間が観測した時点で急にその確率っていうのがどっか行ってしまって「波動関数の収束」という摩訶不思議な現象が起こります。当時、超天才のフォン・ノイマンが、ここを徹底的に追求して、結局、量子力学の理論体系からは「波動関数の収束」なんて現象はどうやっても導出できない!ってことを数学的に証明してしまいます。理論は非常に美しくて整合性もある正しそうだ、でも数学的にありえないことが実際起こっている、結局「人間の意識が波動関数を収縮させる」ということを主張しました。現在では、まあ理由はどうであれ、とにかく収束する、追求しないという「コペンハーゲン解釈」というのがあります。今でも一線の物理学者の多数が支持している解釈かどうなのかは知りませんが、少し昔までは多分これが標準的な解釈だったんでしょう。
一方で、エヴェレットという人が「観測者だけ特別扱いで波動関数の確率の枠組みに入れていないのはおかしくない?」という至極当然の発想で、突き詰めたのが「エヴェレットの多世界解釈」です。
これはつまり、観測者自身も波動関数の確率的存在と考えれば、どこにも観測対象の波動関数の収束みたいなおかしなことが起こる余地はない、理論的に整合が取れている、ということです。
まあ、意識を創発する物質としての人間の脳という観測主体が、量子力学の理論どおりシュレディンガー方程式で記述されるままの波動方程式によって表現されている確率的存在であるならば、それぞれの分布局所で「観測対象が1点に収束している!」と対応する現象が起こってるんでしょ?じゃあそれで矛盾がないじゃない、という考え方です。
意識を創発する物質としての人間の脳という観測主体が確率的に存在している、観測される対象(客体)も確率的に存在している、それぞれ重ね合わさって、「観測対象が1点に収束している!」とそれぞれ辻褄があっている、ってことは、すなわち世界が複数重ね合わさって存在してるってことです。
まあ、普通は信じられませんよね。でも論理的に否定するのは不可能で、論理的にはむしろこっちの多世界解釈のほうがよっぽど辻褄があっています。そもそも「波動関数の収束」みたいな解決不能な問題が解決されている、ってことでこっちのほうが正しそうだ、と私は思うし、今時はかなり多くの(気の利いている)理論物理学者はコペンハーゲン解釈ではなく、多世界解釈じゃないんでしょうか?一般にこれは素朴実在論では「直感」に反する考え方なので、いろいろ理由をつけて否定する人もいるでしょうが、それは理性でもなんでもなく、結局否定することなんて不可能だということくらいのコンセンサスはさすがにできており、だからこそ「コペンハーゲン解釈」「多世界解釈」どちらでもすきな解釈でどうぞ?みたいなことになってるわけです。真実は多世界であったとしても、多世界間は相互作用なんてない(はず)なので、実験で確認することは不可能であり、すなわち反証可能な科学理論としては成立しません。だから科学「理論」の範疇でなく「解釈」の問題です。
多世界解釈は決定論です。一般に馴染みがある、思いっきり俗な言い方をすると運命論みたいなものです。最初からすべては決まっている。
Wikipediaでも
だが、20世紀になると、量子力学におけるコペンハーゲン解釈によって、宇宙は原子下のレベル、量子レベルであまねく確率的であるという説が有力となった。
などと書かれていて、「だから未来は決まっていない」「人間は自分の意志で自由に未来を書き換えられる!」というBackToTheFuture的な世界観がポピュラーなわけですが、ぶっちゃけ、そんな「自由意志」みたいな、物理法則を超越した魔法みたいな事象はないです。意思、意識はこのベイズ理論の先にある「強い人工知能」によって発現すると、現在ほとんどの研究者は確信しており、そうなったら「意識」というか「自己認識」と言う現象も数学的構造あるいは計算結果だと証明されることになるでしょう。
世界は量子力学によって確率統計的に記述されているが、波動関数のランダムな確率的な収束がおこって偶然に決まるのではなく、波動関数で表現されている統計値は宇宙に「もれなく全部」決定的に展開されており、我々はその一部のみを知覚する世界のひとつにいる、ということです。
「波動関数」っていうのはこの世に数学的構造としてひとつしかなくて、それが時間も空間も超越した多世界にわーっとまたがっている、広がっている、その局地局地がある世界のある時間、そしてそこに存在する我々、我々の意識、ということになります。そういうのがいっぱいある、ということです。これが多世界解釈。
コペンハーゲン解釈では、この観測できる世界がまず存在する、まあ素朴実在論の素朴な発想です。そこになんかしらないが、波動関数という数学的「近似」理論があるみたい、それがなんかわからないけど、なんかのきっかけで収束する。この世界にこの波動関数はひとつ!みたいなことになります。間違っていると思いますが。素朴だし。
とこういう「多世界解釈」「決定論」としての哲学的足場が私にはまずあります。
これを前提に「確率論」というのは当然解釈していくわけです。
「ネイマン=ピアソンの頻度主義統計学」の根本的な問題点は、素朴実在論に基づいた「この世界はたったひとつ!」という暗黙の了解、大前提があることです。だから「真の値」とは「神様だけが知っている値」とか、「真の値が存在するが、私達が知る事ができるのは、真の値に近いと思われる値、それがサンプルから計算した平均値や標準偏差だ」みたいな議論になります。まあ日常の主観的には「この世界はたったひとつ!」という気持ちで生活してもまったく問題は発生しないわけですが、数学で突き詰めて考えるときに、果たしてこういう大前提を無条件に暗黙の了解として受け入れて良いのか?といえば良くないと思っています。
多世界解釈を採択する私の世界観からすると、こういう「ネイマン=ピアソンの頻度主義統計学」による「真の値」とは、「時間も空間も超越した多世界にわーっとまたがっている、広がっている、「波動関数」としてこの世に数学的構造として存在している確率分布の最尤値」のことです。
我々がたまたまこの世界で、たまたま観測する、観測できる事象とは、無限の多世界に存在するうち、たまたま今ここで意識を創発していると感じている、という意識がある自分が観測した「今ここでの値」という限定された局所的な値でしかありません。
その「今ここでの値」というローカル値というのは、当然、シュレディンガー方程式の波動関数によって規定される確率分布のどこかにある一つの値であって、確率分布に従って「他にもいっぱい」「今ここでの値」っていうのが決定論的に最初から存在しているわけです。
もうちょっと平たく言うと、
1が出る可能性が100%のサイコロは存在するか?(歪みもないのに)
答えYes。
たしかに歪みがないわけですから、多数回試行すれば、1−6までかなり平均的に出るような「世界」のほうが多世界グループのなかでも圧倒的に多いでしょう。しかしながら、多世界が無限に広がっているわけで、たまたまこの「世界」は「なんだかよくわからないけど、このサイコロは歪みがないのに1ばかり連続して出る!」という世界かもしれません。
あなたが年末ジャンボ宝くじを1枚だけ購入して、「案の定ハズレた!」とあなたが思ってる世界のほうが圧倒的に多いわけですが、「なんだかよくわからないけど、当選したぞ!奇跡だ!」とおもっている世界は2000万分の1の確率で存在するわけです。どこかに。存在しない?なんで?2000万分の1の当選確率であるならば、フェアに考えてそういう確率分布になっているはずです。もちろん、その多世界のうち、「今そこにいるあなた」の脳も確率分布に従って波動関数の重ね合わせで存在しており、意識もそれに呼応しているわけで、その意識において、「なんだかよくわからないけど、当選したぞ!奇跡だ!」と感じる事象になっている確率は2000万分の1にすぎません。
ある事象ひとつをとっても、無限に存在する多世界は、ある波動関数で規定される確率分布ですから、その曲線の山の最も高いところが最も存在確率が高い、つまり世界の数が一番多いです。
そういう多世界のうち世界の数が一番多いだろう(世界の存在確率が一番高いだろう)っていうポイントを「最尤値」と呼びます。
簡単のために次元を落として、オモテウラのコインで考えます。(2面のサイコロっていうのと一緒)(最初からコインの例に統一すればよかったかもしれない)
ネイマン=ピアソンの頻度主義統計学では、オモテが出る確率θは五分五分、1/2=0.5ですね。
一方で、ベイズ統計学ではこんな「オモテが出る確率θは1/2=0.5」みたいな多世界の「最尤値」=「真の値」は初期設定では論じることは不可能です。科学実験としてそんな多世界の全部は到底観測不能だからです。
世界は量子力学の波動関数の確率分布ですべて記述されているのです。まあ、多世界のうち存在確率が一番高いのは、たぶん、θは1/2=0.5、となっている世界だろうね!みたいな確率分布議論しかできません。そして、この世界は、その一番存在確率の高い世界に落とし込まれている可能性が高いから、多分、この世界でもθは1/2=0.5が最尤値となってる確率分布なんじゃない?みたいなことです。
しかし、実際に試行してみて、連続でオモテしか観測されなかった場合、
「おいおい、どうやらこの今自分が生息してる世界は、超多数派のθ1/2=0.5が最尤値の世界のパターンじゃなかったようだ、珍しいね!」ってことになります。
宝くじの例で言い換えると、
「おいおい、当選確率2000万分の一の存在確率が超低い世界なのに、なんか知らないけど、実際にこの世界で当選しちゃったので、この世界はたまたまその存在確率が超低い世界だったみたい!」みたいなことが起こりうるわけです。
今一体何を考えているのか?というと、「確率の確率」を考えています。
ネイマン=ピアソンの頻度主義統計学では「世界はただひとつ」であり、
この世界の「真の確率」もただひとつ、であるわけですが、
ベイズ統計学は多世界解釈であるという見解では、「世界は無数に存在する」ので、
それぞれの世界ごとに、それぞれ確率が存在する、無数に、と解釈できます。
無数に存在するであろう世界のそれぞれの確率を俯瞰的にみて統計的に確率分布で考える、「確率の確率」「確率分布の確率分布」を考えるということがベイズ統計学では可能です。
コインを実際に試行してみて、連続でオモテしか観測されなかった場合は、その世界の観測値に従って
オモテしかでない確率、つまりオモテ確率100%、θ=1が最大値、最尤値になります。
ベイズ推定では、コイン試行の「確率の確率分布」はベータ分布(サイコロなら一般化された多変数のディリクレ分布になる)になり、二次元グラフに表すと、ある世界(この世界)のある時間(観測時点)で、観測結果がオモテ100%だった場合のオモテが出る確率θの分布は、

です。オモテ確率0%、θ=0のときの確率は0になっています。少なくとももう1回はオモテが出たという事象が観測されてしまっているわけで、オモテ確率0%、θ=0というのはもう「絶対にない」ということになります。
さらに連続してオモテが観測されたとき、確率θの分布は、

に変化します。
さらに3回連続でオモテが観測された確率θの分布は、

というように、オモテ確率θ=100%の度合いがどんどん強まっていくことが確認できます。
このまま、「たまたま」オモテしかでない世界だった場合、この延長でどんどん、θの何乗っていうのが1個ずつ増えていってオモテ確率θ=1グラフの度合いが急激になっていくわけです。
さて、仮に、もし次の試行でウラが出たらこの確率分布はどのように変化するでしょうか?

こうなります。
もう、オモテ確率θ=100%というのは、実験、観測で少なくとも、もう1回ウラが出てしまったので、
オモテ確率θ=100%っていうのは「絶対ありえない」0%だ、言い換えると、θ=1.0となる確率はゼロである、というように確率分布が更新されてしまいました。とはいえ当初の実験で3回連続でオモテが観測されていたので、なおオモテ確率のほうが高い分布となっています。
それを打ち消すように、さらにウラが連続して9回出た場合。
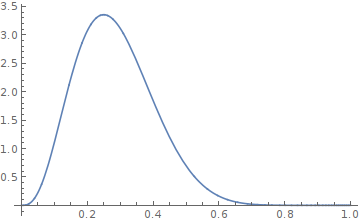
というように確率分布は観測結果に応じて変化していきます。
さらに試行を重ね、オモテ30回、ウラ30回と均等に出るという事象が観測された場合。

かなり「ネイマン=ピアソンの頻度主義統計学」が云うところのいわゆる「真の値」である確率θ=1/2=0.5が際立った確率分布となっています。
多世界が「観測」によって波動関数が収束したように見えることは、ベイズ更新の確率分布をグラフに表したときの領域分割として幾何的にイメージして理解できます。
念の為にまず超基本的な確率のことがらと用語を復習しておきましょう。
P(A,B) = P(A) x P(B|A)「同時確率」P(A,B)は、
事象の確率P(A) に
「条件付き確率」P(B|A)を掛ければ求められる(確率の乗法定理)。
言い換えると、
事象の確率P(A)に掛ければ
「同時確率」P(A,B)になるような確率のことを
「条件付き確率」P(B|A)と定義する。
P(B|A) = P(A,B) / P(A) 条件付き確率と確率の乗法定理は、
定義として表裏一体で同じ概念をそれぞれ逆方向で命名したものです。
非常に単純なことしか言ってないのですが、非常に単純だということがわかりにくい人は、
前回の記事のトランプの例を参照すれば良いでしょう。
カードが黒 ■
カードが赤 □
と表記し、
カードのマーク(スート)の強さは
♠ > ♡ > ♢ > ♣なので、
上位2つを ↑
下位2つを ↓
とグループわけして表記することにする。
| | ■ | □ |
+---|---|---+
| ↑ | ♠ | ♡ |
| ↓ | ♣ | ♢ |Aはカードの色2択(図の横軸)
Bはカードのスートの強弱2択(図の縦軸)
カードの色、黒赤同じ割合の2択の事象の確率
P(A)=1/2で、
カードの色が確定した事象について、さらにそこから、
スートの強弱の同じ割合の2択の事象があるので、
条件付き確率
P(B|A) =1/2となっています。ここまでが大前提。
さて、
♠というスートの存在確率は、
カード色=黒
その上なおかつ
カード強弱=強い
という「条件つき確率」からの「同時確率」で表現できます。
P(A,B) = P(A) x P(B|A)
1/4 = 1/2 x 1/2 そしてよくよく考えてみると興味深いことに、
カードの色A、スートの強弱Bを入れ替えてもまったく同じ論理で、
♠というスートの存在確率は、
カード強弱=強い
その上なおかつ
カード色=黒
という「条件つき確率」からの「同時確率」で表現できます。
P(A,B) = P(B) x P(A|B)なので、「同時確率」P(A,B)について接続してまとめると
P(A) x P(B|A) = P(B) x P(A|B)4つの確率の関係式があります。
簡潔なこの4つの確率の関係式から深淵な理論が導出されてしまう。
P(B|A) = P(B) x P(A|B) / P(A)単に移項しただけなのですが、
この式の形が「ベイズの定理」と特別扱いされて呼ばれています。
ベイズの理論は式を見ての通り徹頭徹尾「条件付き確率についての理論」であると言えます。
ベイズの理論を理解する事は、「条件付き確率」とは何か?を理解することと同じです。
もちろん、こうすればこうなる、ほら使えるでしょ?と道具の使い方だけを学ぶことは可能ですが、
道具の使い方を理解していることは理論の理解ではありませんし、後々苦労するし応用もまったく効かないでしょう。
じゃあ、「条件付き確率」っていうのは多世界解釈において一体どういう意味なんだろう?
と考えてみると、いやいやそれ以前にそもそも「確率」ってなんのことだったんだろう?
と再確認する作業が必要です。
ものごとが「起こる」か「起こらないか」というときに、「可能性」という言葉を使います。
ものごとが起こらないことが観測され確定したときに「可能性が消えた」という言葉遣いをします。
これはすなわちある時点まで不確定であったものが、確定した、ということで、最初から論じている量子力学のコペンハーゲン解釈(この世界は眼の前にある世界唯一つ)で、波動関数がなんか理由がわからないけど、追求するのはあきらめてとにかく事実として収束する、という現象がある、という意味そのものです。(素朴実在論)
一方で、多世界解釈においてはそもそもそんな不確定事象などは存在せず、最初からぜんぶまるごと決定論的に決定されて世界はただそこに存在していて、我々が観測して「事象が確定した!」と思い込んでいるのは、実際のところ我々の脳もその可能性の一つの世界に波動方程式の確率分布のひとつとして存在しており、それぞれの多世界で「観察」した結果「事象が確定した!」と思っているという哲学的立場でした。(プラトニズム)
別の言い方をすると、可能性は消えない、ひとつの可能性を観測した場合、また別の可能性を観測している世界が無数に存在する、世界がそこで分岐したとみなされる。
「分岐」するというと動的な印象がありますが、実際は最初からそのように決定されている数学的構造です。波動関数がそのような確率密度の分布となっており、そのどの部分で切り取って見るか?ということに対応します。
確率とは事象の存在の割合です。世界の存在確率=多世界に含まれている、ある多世界の割合。’
多世界の分量は無限個ある(多分)ので、世界の量は割合でしか表すことはできません。
ブラウザの利用総数なんてわからないけれども、ブラウザ利用シェアは自サイトのアクセス分析から割り出せるみたいなことです。
Chrome7ブラウザからのアクセスは全アクセスのうち70%みたいに。
「こんなパターンの世界が全多世界のうち70%のシェアを占めている」
「こんなパターンの世界の存在確率は70%=0.7である」ということになります。
こういう多世界解釈の世界観でベイズ理論はどう解釈できるか?ということを追求してみます。
ベイズの定理
P(B|A) = P(B) x P(A|B) / P(A)ベイズ理論風に記号を書き直す
AをEvidence(証拠、観測値、データ(の確率分布))
BをHypothesis(仮説(の確率分布))
と書き換えて、
P(H|E) = P(H,E) / P(E)
= P(H) x P(E|H) / P(E)この確率と条件付き確率の関係式を多世界解釈の立場から「理解」して「イメージ」できることを目標とします。
ベイズの定理の式がこうだから論理的にこうなる、という説明の組み立てはしない、すべきではないので、いったんこの目標を確認した上で、最後に統合します。
すでに上のほうで一回説明を試みた、コイン投下の試行について思考実験します。
まず多世界があります。その無限に広がる多世界のうち「今これからコインの実験をしよう!」とあるコインを用意した世界がそのなかに存在しています。そしてもちろん「コイン?なにそれ?」というまったくこの試行に無関係の世界がその他無限に存在していますが、そこは関係ないので今回切り捨てます。
あるコインについてだけの多世界にまず絞り込みます。これを「全事象」と初期設定します。わかりますね?
これからそのひとつのコインに関する多世界にまたがって思考実験していくわけですが、あるひとつの世界のなかで科学的な実験を行った場合、観測可能なのはたかだかその世界に所属しているコインひとつだけです。
それ以外の他の世界に所属している科学実験のことは絶対に観測不可能です。知る手段はありません。それぞれの世界の観測は独立しています。
ただし、量子力学がものがたるように、世界は量子力学の波動関数の確率分布ですべて記述されています。数学を通じて多世界にまがたる確率分布の議論をすることが可能ですし、それをやってるのが量子力学であるといえます。
それぞれの世界にはそれぞれの世界特有の観測結果や確率がありますが、多世界なので、前述したとおり、Chrome7ブラウザからのアクセスは全アクセスのうち70%みたいに、
「こんなパターンの世界が全多世界のうち70%のシェアを占めている」
「こんなパターンの世界の存在確率は70%=0.7である」という話ができます。
「確率の確率」です。もうちょっというとシェアの話なので、確率の確率分布の話ができます。
逆に言うと、多世界について我々が数学を通じて話せるのは、多世界の「確率の確率分布」以外にはありません。その話しかできないし、その話だけを徹頭徹尾しているのがベイズ統計学です。
あるコインについてのみ切り出した多世界の全事象を以下のように表現することとします。
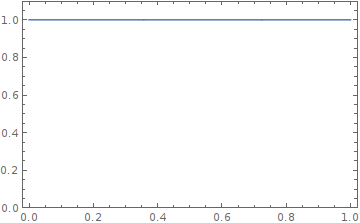
横軸は0-1.0 の確率
縦軸も0-1.0 の確率
確率の確率のグラフです。
全事象は確率100%なので、掛け合わせると1.0になっています。
このグラフでは、確率の確率分布が視覚的に把握できます。
現在よく見ると、y=1 で直線が引かれており、
xとyともに0-1区間の領域で四角形になっていますね。
この領域があるコインについてのみ切り出した多世界の全事象で1となっています。
全事象のシェアは100%ということです。
ここで、コインを1回投げます。
ある世界ではオモテが出た。ある世界ではウラが出た。
コインを投げると、その観測結果を境界として多世界が分岐します。

このように分割されます。
y=x という直線で四角形の領域が半分に分割されました。
1回目の試行でオモテが出たほうの多世界グループと
1回目の試行でウラが出たほうの多世界グループと
に多世界全事象が半分に分割されました。
右下の三角形の領域がオモテ世界で、この世界の目線からすると、
1回目の試行でオモテが出た、という観測結果が確定したことにより、
1回目の試行でウラがでる、という「可能性は消滅した」ということになります。
しかしながら、「可能性は消滅などしない」というのが多世界解釈でした。
オモテ世界から消滅したように見えた、可能世界であるウラ世界は、
このグラフの左上の三角形の領域です。
彼らからすると、可能性が消滅したように見えるのはむしろオモテ世界のほうです。
全領域
y=1

から
オモテ世界の領域
y = x

を引き算してやると、
ウラ世界の領域
y = 1 - x

左上の三角形の領域(の面積)がちょうど上下ひっくり返って明示的な確率の関数として計算して表現できます。
ちなみにこれは全領域1のうちの割合なんぼという話なので、
「確率の密度」という解釈ができるので、「確率密度関数」と呼ばれています。
全領域1のうちの割合なんぼという「確率の密度」を総計していけば、当然
全領域1のうちの割合なんぼが計算できるので、
「確率密度関数」を積分すれば確率になります。
2回目の試行をします。
1回目の試行と2回目の試行はコインを投げるということでまったく同じことの繰り返しです。
つまり、世界をコインを投げることによってまた

このように分岐させてしまうわけです。
ただし!分岐するのは、すでに分岐してしまった世界の延長で分岐します。すでに分岐してしまった世界がふたたび統合されたり、なかったこと、チャラになることはありません。最初から決定されているであろう多世界の分岐構造をひたすら辿っていく確認作業をやっているだけなので、分岐をたどっていったはずなのに、元の分岐がチャラになったという動的な変更は起こりえない、ということです。

を前提とした上で、

で、さらにまた分岐する。これはすなわち「条件付き確率」のアレをやっているということです。
P(A,B) = P(B) x P(A|B)前提となる事象に「条件付き確率」を乗算すれば、「同時確率」すなわち「分岐後の世界の確率」が得られる。
実は最初に、
全領域
y=1

に「条件付き確率」
y = x

y = 1 かける xと乗算した結果、
y = x

になっていたのでした。
すでに世界は、
1回目オモテ世界
1回目ウラ世界
のふたつに分岐されてしまっていますが、全パターンの分岐を辿るのはしんどいので、
当面、1回目オモテ世界の延長の分岐だけを探ることとします。
1回目オモテ世界の延長で、
1回目オモテ世界を前提に、条件付き確率の乗法定理を適用し
P(A,B) = P(B) x P(A|B)今回さらにまたxを乗算するので、
で分岐(グラフが分割)されます。

y=x で表される確率密度関数の領域をさらにまた、y=x で表される確率密度関数で表される条件付き確率という「割合」をもって分割したら、乗算して二次関数となって分割されることになります。
1回目オモテ世界の延長で、
オモテ連続2回世界は、一番右下の三角形が凹んだような領域に分類されます。
これは、最初の方で説明した、
さらに連続してオモテが観測されたとき、確率θの分布は、

に変化します。
と同じですね。係数の3がないのは、今回分岐大元のコイン多世界全事象=1のままで考えているからです。これはあとでどうせまた説明することになります。
じゃあ、その世界から可能性が消滅したように見えて実は別の世界に分岐されている、
1回目オモテ世界
2回目ウラ世界
という世界は、グラフ中央の三日月みたいな領域に分類されています。
すでにやったように、単なる引き算でもうちょっと明示的に確率密度関数として表現できますから、
y=x から 二次関数を引き算してみる、
変形すると
これもどっかでみたことありますね?

例のベータ分布になってしまいました。
1回目オモテ
2回目ウラ
というイーブンの観測結果であると、最尤度0.5のベータ分布です。
ここで、念の為に確認ですが、
我々が数学を通じて多世界について語れるのは、せいぜい確率の確率分布でしかありません。
このように多世界の初期設定をして、そこから観測結果に応じて多世界の分岐をたどっていったとしても、その世界自体も、また次なる分岐に備える、確率分布で記述されている多世界でしかありません。
多世界→多世界→多世界→多世界→多世界→
と延々と連なっているので、事象観測後の分岐した世界で語れるのは、
分岐前と同じような確率の確率分布のはなしだけです。
さて、さらに多世界分岐の探求をつづけます。
で分岐(グラフが分割)

されましたが、そのうち、オモテ連続2回世界の延長の分岐を探ります。
グラフでいうと、一番右下の三角形が凹んだ領域のことです。
オモテ連続2回世界の延長を前提とし、
また同じ試行の
「条件付き確率」
y = x

によって世界が分割されるので、

となります。
オモテ連続2回世界の延長で、分岐したもう片方の
3回目ウラ世界は、
グラフの一番細い三日月みたいな領域に分類されています。
オモテ連続2回世界ー 3回目オモテ世界 という引き算で確率密度関数を求めると、
変形すると

これも当然のごとくベータ分布になっていますね。
もうあとは同じことの繰り返しが延々と続きます。
そしてすべての分岐のパターンで限りなく世界が分岐、分割され細分化していきます。
最初の方で確認した
それを打ち消すように、さらにウラが連続して9回出た場合。

というように確率分布は観測結果に応じて変化していきます。
さらに試行を重ね、オモテ30回、ウラ30回と均等に出るという事象が観測された場合。

以上のような確率分布になるような観測結果をもつ世界はこの全事象の分岐(領域の分割)の先のいずれかのひとつとして存在しています。
だいたい世界観のイメージは伝わったと思いますので、観測による多世界の分岐現象がベイズの定理でどう表現されているか確認します。
Evidence(証拠、観測値、データ(の確率分布))
Hypothesis(仮説(の確率分布))
P(H|E) = P(H,E) / P(E)
= P(H) x P(E|H) / P(E)というものでした。
モデルケースとして、以下を再掲します。
で分岐(グラフが分割)

されましたが、そのうち、オモテ連続2回世界の延長の分岐を探ります。
グラフでいうと、一番右下の三角形が凹んだ領域のことです。
オモテ連続2回世界の延長を前提とし、
また同じ試行の
「条件付き確率」
y = x

によって世界が分割されるので、

以上を例にとって考えてみると、
1.事前確率(分布)
観測によって分岐される前の前提となる世界の分布
この場合は、オモテ連続2回世界がP(H)という事前確率分布になっている
2.観測(分布) 一般的には「尤度(Likelihood)」という用語になっている
観測による分岐前を前提とした条件付き確率の分布、
事前確率(分布)であるP(H)を前提としたときの観測データEvidenceの確率分布
この場合は、試行データ=オモテ
3.事後確率(分布)
観測データEvidenceによって分岐した後の世界の確率分布、
これは、観測データEvidenceを前提とした条件付き確率の分布として表現されている
この場合は、オモテ連続3回世界の確率分布が得られた
さて、最後に、ベイズの定理
P(H|E) = P(H) x P(E|H) / P(E)4つ目の確率分布である、 P(E)です。
初見では
「これこそがEvidenceの確率なのだから観測のなにかの分布なんだろう?」
と勘違いしてしまいますが、すでに確認したとおり、観測に該当するのは
世界が分岐する前の、事前確率分布P(H)を前提とした、
条件つき確率分布であるP(E|H)のほうでした。
今回、多世界解釈に基づいて、
あるコインを試行するときの多世界の全部を全事象1として、
それが観測によって分岐、分割されていくという現象を調べました。
その結果、世界が分岐し、確率密度のグラフ領域が分割された先のひとつには、
たとえば、オモテ1回ウラ1回のイーブンな観測が得られた世界の確率分布が、

このようになっていることも確かめられました。
この確率分布は、あくまで、
あるコインを試行するときの多世界の全部を全事象1としたときのグラフのうち

中央の三日月のような領域として分割された割合です。
さあここで、よくわかった、でももう多世界全部の事象のことは関係ないや、この分岐した世界ローカルで考えたい!という立場を取る方針にした場合、
あるいは、
多世界分岐後の新たなる多世界の出発点として、この分布こそが今ここにあるコイン試行世界のすべてであり、原点である、という方針にした場合、
つまり、
多世界の全事象、全領域

ではなく、
多世界の全事象、全領域

という初期設定にリセットしたい場合、
この確率密度関数の積分値が1となるように調整しなおさなければなりません。
これを「正規化(Normalization)」と言い、これは量子力学の波動関数でも同じ操作が必要になります。確率っていうのはしょせん、何かを基準とした割合のことなんで、どこを基準に取るか?っていうので値を調整する必要がでてきます。
ちなみに、ベイズ理論において、この確率密度関数の積分っていうのがめちゃくちゃ面倒くさい場合が多くて、うまい近似の手法でやったり、代数的な計算はあきらめてMCMCというモンテカルロ・シミュレーション(サンプリング)の手法でやったり、いろいろ工夫があってこういう積分の計算方法だけで一大研究課題となっています。
今回のケースでは、世界をベータ分布の連鎖で分割していったので、かなりはっきりとした代数のルールがあり、積分する必要はありません。(自然な共役分布)
しかし、その代わり、その操作の履歴データが必要となります。
というベータ関数にまつわる公式を利用すると、
全多世界事象1のうち、

三日月部分の世界の領域の割合は、1/6である、ということがわかります。
これが、全事象1のうちEvidenceの割合なので、P(E)の値となります。
じゃあ、P(E)が全事象となるようにリセットしたい、正規化したいならば、
全事象1のうちEvidenceの割合であるP(E)で割り算すればリセットできますね。
を正規化すると、

係数が1から6に増えたことによりグラフの領域が拡大されたことが確認できます。
4.全事象のうちの事後確率(分布)の確率
P(E) とは最初設定した全事象にたいする、事後分布P(H|E)の確率
これは多世界分岐(ベイズ更新)のすべての履歴が必要となる。
あるいは履歴なしでは積分して1になるような値を求める必要があるので、計算が一番やっかい。
P(H|E)を全事象としてリセットする正規化のために必要。
ベータ分布で
のモデルケースでは、
となり、
のモデルケースでは、
になる。
以上で、
ベイズの定理
P(H|E) = P(H) x P(E|H) / P(E)の4つの確率(分布)がすべて出揃いました。
ある確率分布で記述されている多世界があり、データを観測し、それに応じて世界が分岐し、確率(シェア、領域の割合)が分割され、分岐後の多世界がそれぞれ持つ確率分布を得る、ということをベイズ更新(Bayesian Updating)といいます。量子力学の多世界解釈すれば、ということですが。
いずれにせよ、この観測結果を反映するベイズ更新が連鎖構造になっています。
量子力学の確率分布であらわされる多世界が観測結果を反映して分岐している構造と1:1に呼応しています。
さらに試行を重ね、オモテ30回、ウラ30回と均等に出るという事象が観測された場合。

という様に、係数がめちゃくちゃ大きな値となっているのは、そもそもの全事象から世界が分割されまくった確率分布をリセットして正規化したからだ、という自然な解釈ができます。
以上は、コインの試行についてベータ分布になる、というのはどこにでも普通に書かれている知見ですが、量子力学の確率理論、特に多世界解釈で、ベイズ理論を俯瞰してみればどういう意味だろう?というのは筆者のオリジナルです。別にどこか他のどなたが同じ解説をしているかもしれませんが、よくわかりません。
特に、ベイズ理論を確率分布に適用した場合についての尤度(Likelihood)について納得できる解説が見当たらなかったのですが、こう俯瞰したら納得できたということです。また、ベイズ統計学について、「主観確率」であるとか「あいまいな推定ができる」とか、「信念の度合いが表現できる」とか事例を示されたとしても、それが数式のイメージとして腑に落ちることはありませんでした。
また、世紀をまたいで継続している、「ネイマン=ピアソンの頻度主義統計学」とベイズ統計学の論争は、根本的にはこのコペンハーゲン解釈と多世界解釈の問題があると考えています。
そして念の為ですが、今回書いたような多世界解釈の哲学的立場は、素朴実在論では到底受け入れられないために不当な心理的反発を招きやすいのですが、これはもちろん私の独自哲学でもなんでもありません。今回あくまで多世界解釈の哲学的立場をそのまま援用してベイズ統計学を解釈してみた、という論理的帰結にすぎません。量子力学において波動関数(確率密度関数)で量子の存在確率が定まる、それは観測という行為にリンクしているというのは、ベイズ更新の特徴そのものであり、照らし合わせてみると案の定自然に解釈できた、ということにすぎません。
基本的に義務教育あるいは高等教育であっても多世界解釈を教えることは「何かと面倒くさい」ことのようで、理由とすれば素朴実在論的世界観が妨害しているとしか思えないのですが、その一方で素朴実在論と相容れない相対性理論、量子力学は学習する必要はあります。
その際、いずれにせよ「観測の結果、可能性が消えた」と普段発している言葉の意味はいったいどういうことなのか?というのは別段ベイズ統計学に限らず義務教育で習う局面であっても誰でもが一度は考えたことがあるかもしれません。「観測の結果、可能性が消えた」というのは量子力学の波動関数の収束に他ならず、これはコペンハーゲン解釈では理論的に破綻していることは数学的に証明されています。理論内からけして導出できない現象について理論の外に大業な名前をもって原理の追加する、ことがまかり通るのであればあらゆるオカルト現象も同様に、なんか大業な名前をつけてそういう原理の法則であると言ってしまえばすむわけなので、これは科学ではないだろうと訝しく思っています。
この「観測の結果、可能性が消えた」というのは、実際ベイズ更新の解説で多用されていること、あと、ベイズ理論から展開されるベイズ統計学的機械学習が最近主流になりつつありますが、次にどの方向に進めばスムーズに楽しくすすめるのか?過去の自分の経験を踏まえながら少し紹介します。
今回紹介したとおり、ベイズ推定はデータを観測して条件付き確率で確率分布をアップデートする連鎖構造になっています。この簡潔な連鎖構造を応用していくらでも複雑な構造化が可能なのですが、視覚的に表現する体系が確立されていて、グラフィカルモデルといいます。
グラフィカルモデルのノードひとつひとつが条件付き確率からのベイズ推定であり、グラフィカルモデルのネットワーク構造はベイズ推定のネットワークです。
矢印ある有向ならばいわゆるベイジアンネットワークであり、無向ならマルコフ確率場です。
マルコフ確率場とだけ聞くとなんか面倒くさそうだな、と思うんですが、構造としてはこちらのほうがベイジアンネットワークよりもシンプルで、まあベイズで連想記憶とかやる場合はこちらを確実に使うでしょう。あとコンピュータビジョン。
逆にグラフィカルモデルの「ことば」が理解できないと、たいていの本を読むとき必ず挫折してしまうので、ベイズの基本を徹底的に学習したその次はグラフィカルモデルに進むというのがおすすめです。
PRMLはベイズ統計学に基づいたグラフィカルモデルと生成モデルの体系的な説明が以前から評価を得た大きな理由だと思いますが、
著者のビショップ教授もグラフィカルモデルは導入として特別扱いしているようで、
PRMLの8章グラフィカルモデルだけは無償でPDFダウンロードできるようになっていたり、
http://research.microsoft.com/en-us/um/people/cmbishop/prml/
Contents list and sample chapter (Chapter 8: Graphical Models) in PDF format.
http://research.microsoft.com/en-us/um/people/cmbishop/prml/pdf/Bishop-PRML-sample.pdf
サマースクールでもその無償PDFをテクストとして、数学とりのぞいたバージョンの導入レクチャーをやっていてYouTubeで閲覧できます。見なきゃ損のコンテンツ。
講義のスライドもダウンロードできます。
http://mlss.tuebingen.mpg.de/2013/bishop_slides.pdf
非常にいたれりつくせりで、英語も聞き取りやすいのですが、耳障りが良すぎて寝る人が多い気がします。
Graphical Models 1 - Christopher Bishop - MLSS 2013 Tübingen
https://www.youtube.com/watch?v=ju1Grt2hdko
Graphical Models 2 - Christopher Bishop - MLSS 2013 Tübingen
https://www.youtube.com/watch?v=c0AWH5UFyOk
Graphical Models 3 - Christopher Bishop - MLSS 2013 Tübingen
https://www.youtube.com/watch?v=QJSEQeH40hM
このビショップ講義でも、グラフィカルモデルの基本としてのベイズ推定で「可能性が消える」話をたくさんしています。上のスライドみれば多分それはすぐわかるでしょう。
あとYoutubeで
Graphical Modelsで検索すれば、この界隈の著名人によるグラフィカルモデルの講義が沢山あります。Daphne Kollerとか。
https://www.youtube.com/watch?v=WPSQfOkb1M8&list=PL50E6E80E8525B59C
こっちは「長い」膨大な量で自分もまだ全部見れていません。
もちろん、前回紹介したサイモン・プリンスの
「ベイズ推定とグラフィカルモデル:コンピュータビジョン基礎」
もこの流れとなります。これも実質日本語訳の秀逸なオンライン講義が広島大のToru Tamaki 先生のレクチャーで見れるのでした。実際これはオンライン講義のほうがわかりやすくて、本読むのより随分楽です。
最近多いですねこういう優良な無料学習コンテンツが。
こういう秀逸なコンテンツを複数あわせて読む、聞く、見ると、多分最短で結構なところまで進めるんじゃないでしょうか。
本は速読したり、スキャン的な読解が可能で、内容が薄いとオンラインビデオチュートリアルなんかより本のほうが便利なんですが、思ったのはこういう一般にはとっつきにくい内容であるほど、著者は書籍より内容を一般向けに噛み砕いて非常に熱心に親切に教えようとする人が多いってことです。ああこれならもう本文読まなくていいんじゃない?という感じだったり、そう思ってから本文読むと、楽に読めたり、もちろん数式などはさっきのPRML8章みたいに、書籍には書いてあるみたいなことがあるんですが、どっちにせよ先にオンライン見たほうが良いと思います。